2nd Derivative Test For Extrema

We know that every monotonic function assumes its minimum or maximum value at the endpoints of the domain'south definition of the function. A more comprehensive result is "Every continuous office on a closed interval has a minimum value and a maximum value". A critical point of the function f is the indicate c in the domain of a office f at which f′(c) = 0 or f is not differentiable. Also, if f is continuous at c and f′(c) = 0, then there exists an h > 0 such that f is differentiable in the interval (c – h, c + h). In this article, you lot will learn the working rule for finding the points of local maxima or local minima points, i.due east. maxima and minima, with the help of only the first-order derivatives.

A derivative exam applies the derivatives of a role to decide the critical points and conclude whether each signal is a local maximum, a local minimum, or a saddle betoken. Derivative tests, i.e. the commencement and second derivative tests, tin can also give data regarding the functions' concavity. Now, go through the first derivative test definition and how it is used to find the local maxima or local minima.

What is the First Derivative Exam?

The start-derivative test examines the monotonic properties that indicate where it increases or decreases, focusing on a particular point in its domain of the function. These can exist observed from the following facts.

If the given function changes from increasing to decreasing, the office volition achieve the highest or maximum value at the respective point.
If the given function changes from decreasing to increasing, it will accomplish the most negligible or minimum value at the respective point.
If the given function fails to change, i.east. remains increasing or remains to decrease, then no highest or most negligible value (i.eastward. least value) is obtained.

First Derivative Test for Maxima and Minima

Mathematically, we tin can derive the outset derivative test to find the local maxima and local minima of a function using the critical signal and the kickoff derivative of the function.

Suppose f is a part defined on an open interval I and continuous at a disquisitional point c in I. And so, we can decide the local maxima, local minima, and inflection betoken every bit given below.

First Derivative Test

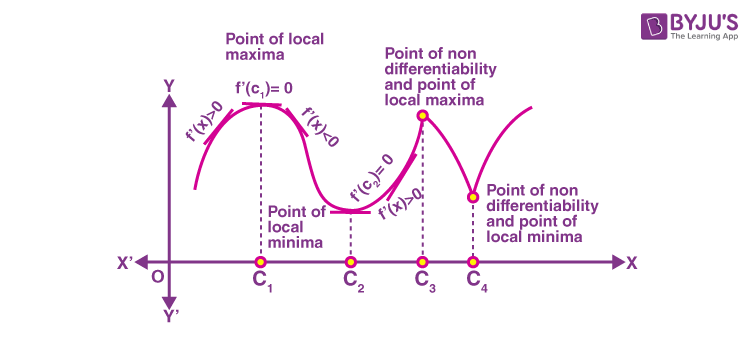
Local Maxima

The critical indicate c is called the signal of local maxima if f′(ten) changes the sign from positive to negative every bit ten increases through c. In other words, if f′(10) > 0 at every point is fairly shut to and to the left of c, and f′(x) < 0 at every signal close enough to and to the correct of c, then c is the local maxima.

Local Minima

The critical betoken c is chosen the betoken of local maxima if f′(10) changes the sign from negative to positive to negative as ten increases through c. In other words, if f′(10) < 0 at every point is close enough to and to the left of c, and f′(10) > 0 at every point is close plenty to and to the correct of c, then c is the local minima.

Point of inflection

If f′(x) does not change the sign equally x increases through c, then c is neither a point of local maxima nor a point of local minima. However, such a point is called the betoken of inflection.

Too, check: Maxima and Minima Using First Derivative Test

Beginning Derivative Test Steps

Beneath are the steps involved in finding the local maxima and local minima of a given function f(x) using the commencement derivative test.

Step one: Evaluate the get-go derivative of f(10), i.e. f'(10)

Step 2: Place the critical points, i.east.value(s) of c by assuming f'(x) = 0

Pace 3: Clarify the intervals where the given function is increasing or decreasing

Stride four: Determine the extreme points, i.due east. local maxima or minima

Starting time Derivative Examination Instance

Question:

Find local maximum and local minimum values of the role f given by f(x) = 3x⁴ + 4x³ – 12x² + 12 using the starting time derivative test.

Solution:

Given,

f(x) = 3x⁴ + 4x³ – 12xⁱⁱ + 12

Pace 1: Evaluate the starting time derivative of f(10), i.e. f'(10)

f'(x) = (d/dx)[3x⁴ + 4xⁱⁱⁱ – 12x^two + 12]

= iii(4xⁱⁱⁱ) + 4(3xⁱⁱ) – 12(2x) + 0

= 12x³ + 12x² – 24x

= 12x(x² + x – 2)

= 12x(x² + 2x – x – 2)

= 12x[x(x + ii) – 1(x + 2)]

= 12x(ten – 1)(x + 2)

Thus, f'(x) = 12x(x – i)(x + 2)

Step 2: Identify the disquisitional points, i.eastward.value(south) of c by assuming f'(x) = 0

i.e. 12x(x – 1)(x + 2) = 0

x = 0, x – i = 0 or x + 2 = 0

That means, f'(x) = 0 at x = 0, 10 = ane and 10 = -2.

Therefore, the disquisitional points are -two, 0, and 1.

Step 3: Analyze the intervals where the given function is increasing or decreasing

Interval	Sign	Behaviour of the function
-∞ < x < -two	f'(x) < 0	Decreasing
10 = -ii	f'(x) = 0	Minimum
-2 < x < 0	f'(x) > 0	Increasing
x = 0	f'(ten) = 0	maximum
0 < x < one	f'(x) < 0	Decreasing
x = 1	f'(x) = 0	Minimum
1 < x < ∞	f'(x) > 0	Increasing

These intervals and behaviour of the function tin can exist observed from the graph of f(10) given below:

First Derivative Test Example

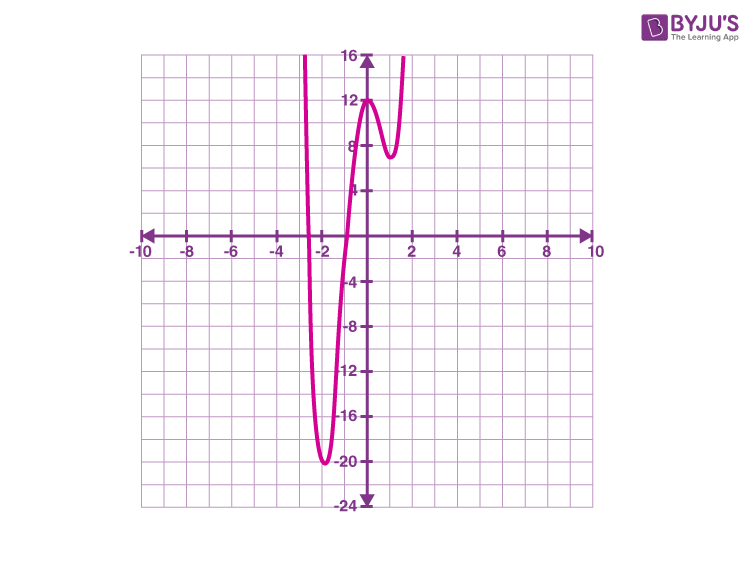
That ways,

f'(x) > 0; -2 < x < 0 or x >one

f'(x) < 0; x < -2 or 0 < x < i

Step four: Determine the extreme points, i.e. local maxima or minima

Substituting ten = -two in f(10),

f(-2) = 3(-2)⁴ + 4(-ii)^three – 12(-2)ⁱⁱ + 12

= 48 – 32 – 48 + 12

= -20

Minimum indicate = (-2, -20)

Substituting x = 0 in f(x),

f(0) = iii(0)^four + 4(0)³ – 12(0)² + 12 = 12

Maximum point = (0, 12)

Substituting x = ane in f(x),

f(1) = 3(one)⁴ + four(1)³ – 12(1)² + 12

= iii + iv – 12 + 12

= seven

Minimum point = (1, 7)

Hence, the local extreme points are:

Local minimum = (-2, -xx) and (1, 7)

Local maxima = (0, 12)

Often Asked Questions – FAQs

Give an case for the start derivative.

Velocity is an example for the kickoff derivative. It is a derivative of position relative to time.

We tin can use Fermat's theorem on Maximum and minimum derivatives of differentiable functions. True or Fake?

True. Fermat's theorem can be used to observe the maximum and minimum derivatives of differentiable functions.

Requite example for existent life derivative.

Real life examples of derivatives are turn a profit maximization, loss minimization in any business organisation, Temperature variations, speed in races to calculate winning.

What does information technology hateful when the first derivative is positive?

If the part is increasing then the get-go derivative is positive.

The first derivative is less than zip. What does this imply?

If the commencement derivative is less than cypher, and then the role is decreasing.